

Bei diesem Verfahren, dem Sieb des Eratosthenes, handelt es sich streng genommen nicht um einen Test im zuvor beschriebenen Sinne. Vielmehr dient das Verfahren dazu, alle Primzahlen bis zu einem bestimmten Grenzwert zu bestimmen. Aus der Liste der so ermittelten Primzahlen kann allerdings anschließend ein zufällig gewählter Wert ausgesucht werden. Dieses sehr einfache Verfahren funktioniert nicht effizient für große Primzahlen. Daher kommt es in der Kryptografie nicht zum Einsatz. Dennoch eignet es sich sehr gut für die Bestimmung von kleineren Primzahlen und ist insbesondere sehr einfach zu verstehen und anzuwenden. Das Vorgehen dieses Verfahrens ist wie folgt:
Man wählt einen Maximalwert \(n \in \mathbb{N}\) mit \(n \geq 2\) und notiert alle Zahlen \(2, 3, 4, \dots, n\) in einer Liste. Jede Zahl erhält eine Markierung, die anzeigt, ob es sich um eine Primzahl oder um eine zusammengesetzte Zahl handelt. Zunächst sind alle Zahlen unmarkiert und somit potenzielle Primzahlen. Das Verfahren läuft nun iterativ wie folgt:
Beispiel: Sieb des Eratosthenes
Wir wählen \(n := 100\) und bestimmen alle Primzahlen zwischen \(2\) und \(n\). Hierzu tragen wir alle Zahlen \(2, 3, \dots , n\) in
eine Liste ein. Zunächst sind alle Einträge unmarkiert und damit potenzielle Primzahlen.
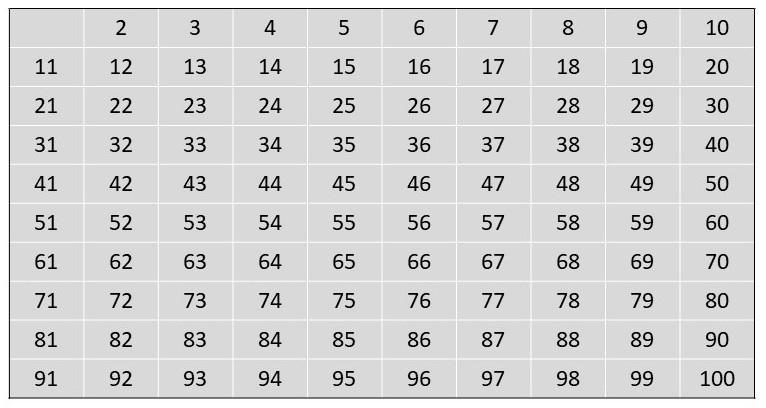
Die kleinste unmarkierte Zahl ist die 2. Diese ist offenbar eine Primzahl, also markieren wir sie als solche. Anschließend markieren wir
alle Vielfachen von 2, also 4, 6, 8, 10, 12, ..., 96, 98, 100, als zusammengesetzte Zahlen.
(Primzahlen werden in diesem Beispiel dunkelblau markiert, zusammengesetzte Zahlen hellblau)
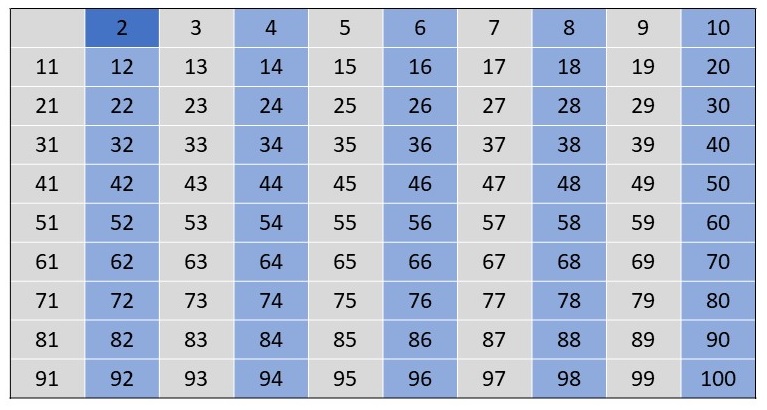
Die nächste unmarkierte Zahl ist die 3. Diese ist offenbar wieder eine Primzahl, also markieren wir sie entsprechend. Weiterhin markieren
wir alle Vielfachen von 3 als zusammengesetzte Zahlen. Wir können hierbei tatsächlich mit dem Quadrat von 3, also mit der Zahl
\(3^2 = 9\), beginnen, weil die kleineren Vielfachen bereits betrachtet wurden (denn sie sind stets auch Vielfache von kleineren Zahlen). In
diesem Fall ist die 6 zwar ein Vielfaches von 3, aber mit \(3 \cdot 2 = 6\) ebenso von 2, und damit bereits als zusammengesetzte Zahl markiert.
Die nachstehende Abbildung zeigt den Zustand der Liste, nach der Markierung von 3 als Primzahl und der Markierung aller Vielfachen von 3, also
9, 12, 15, ..., 93, 96, 99, als zusammengesetzte Zahlen.
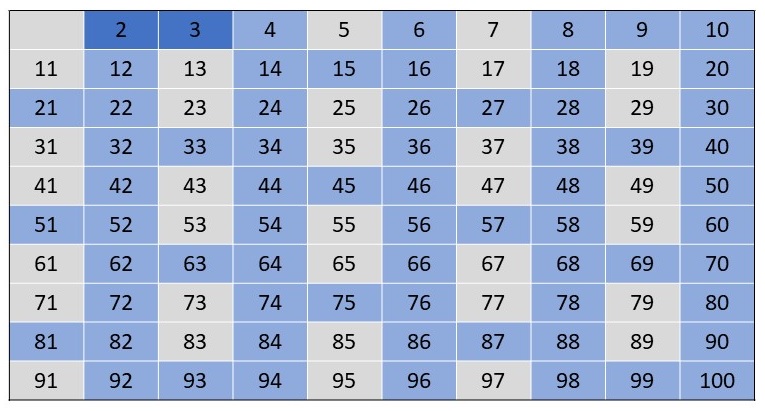
Als nächste unmarkierte Zahl betrachten wir die 5. Diese ist wiederum eine Primzahl. Wir markieren sie als solche und anschließend alle
Vielfachen von 5 als zusammengesetzte Zahlen. Auch hierbei können wir wieder mit dem Quadrat, also mit \(5^2 = 25\), beginnen, weil alle
kleineren Vielfachen von 5 bereits Vielfache kleinerer Zahlen sind (es ist \(5 \cdot 2 = 10\) und \(5 \cdot 3 = 15\)). Nach der Markierung von
5 als Primzahl und aller Vielfachen von 5, also 25, 30, 35, ..., 90, 95, 100, als zusammengesetzte Zahlen, erhalten wir den nachstehend
gezeigten Zustand.
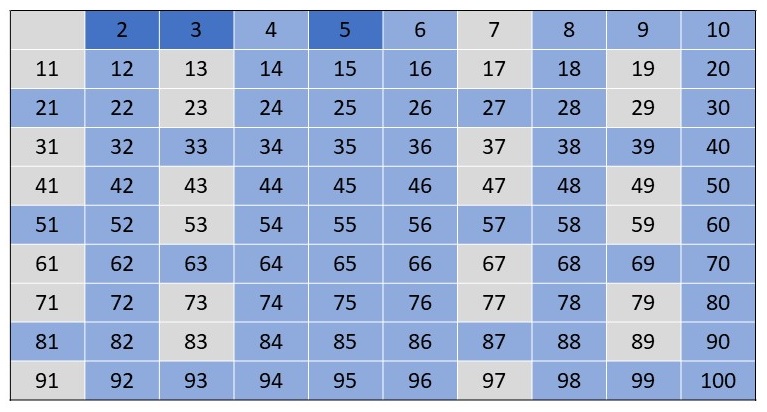
Die nächste unmarkierte Zahl ist die 7. Offenbar handelt es sich wieder um eine Primzahl. Daher markieren wir die 7 entsprechend und
markieren anschließend alle Vielfachen von 7 als zusammengesetzte Zahlen. Wiederum können wir mit dem Quadrat, also mit \(7^2 = 49\),
beginnen, weil die kleineren Vielfachen bereits Vielfache kleinerer Zahlen sind (es ist \(7 \cdot 2 = 14, 7 \cdot 3 = 21, 7 \cdot 4 = 28,
7 \cdot 5 = 35\) und \(7 \cdot 6 = 42\)). Die folgende Abbildung zeigt die Liste nach der Markierung von 7 als Primzahl und der Markierung
der Vielfachen, also 49, 56, 63, ..., 84, 91, 98, als zusammengesetzte Zahlen.
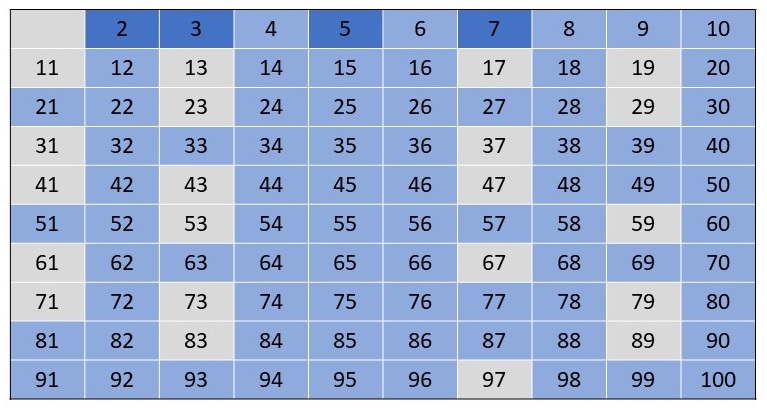
Die nächste unmarkierte Zahl ist die 11 - wiederum eine Primzahl. Weil \(11^2 = 121 \gt 100\) ist, wurden alle zusammengesetzten Zahlen
\(\leq n\) betrachtet und wir können das Verfahren abbrechen. Alle bisher nicht markierten Zahlen sind somit offenbar ebenfalls
Primzahlen. Die nachstehende Abbildung zeigt die finale Liste nach Abschluss des Verfahrens.

Wie man sieht, ist das Sieb des Eratosthenes ein sehr einfach anzuwendendes Verfahren, welches insbesondere zur Bestimmung kleiner Primzahlen sehr gut geeignet ist. In der Praxis benötigt man für Kryptoverfahren allerdings häufig enorm große Zahlen. Daher wollen wir im Folgenden noch einen zweiten Primzahltest vorstellen, der sich auch für sehr große Zahlen eignet und in der Praxis bei Kryptoverfahren tatsächlich zum Einsatz kommt. Es handelt sich - wie übrigens bei den meisten effizienten Primzahltests - um einen sogenannten probabilistischen Test. Das bedeutet, wenn die betrachtete Zahl den Test nicht besteht, so ist sie mit Sicherheit aus Faktoren zusammengesetzt (die Faktoren werden dabei allerdings nicht bestimmt). Andernfalls handelt es sich mit einer gewissen Wahrscheinlichkeit um eine Primzahl. Indem man den Test mehrmals durchführt, kann man die Wahrscheinlichkeit, dass die betrachtete Zahl wirklich eine Primzahl ist, entsprechend maximieren. Auch wenn man zunächst nicht den Eindruck haben mag, sind diese Art von Tests für die Praxis tatsächlich vollkommen ausreichend.
Bevor wir den eigentlichen Primzahltest vorstellen, müssen wir zuvor noch den Begriff der sogenannten Carmichael-Zahlen einführen, der für das weitere Verständnis erforderlich ist.
Eine zusammengesetzte Zahl \(n \in \mathbb{N}\) heißt Carmichael-Zahl, falls für alle \(b \in (\mathbb{Z}/n\mathbb{Z})^\times\) gilt: \(b^{n-1}\:mod\: n = 1\).
Sei \(p \in \mathbb{N}, p \gt 1\) die Zahl, für die getestet werden soll, ob es sich um eine Primzahl handelt. Wir wählen zufällig ein \(x \in \mathbb{N}\) mit \(0 \lt x \lt p\).
Falls \(ggT(x, p) \not = 1\), hat \(p\) einen Teiler \(d\) mit \(1 \lt d \leq x \lt p\). Folglich ist \(p\) eine zusammengesetzte Zahl.
Falls \(ggT(x, p) = 1\), betrachten wir \(x^{p-1}\:mod\:p\).
Falls \(x^{p-1}\:mod\:p \not = 1\), ist \(p\) eine zusammengesetzte Zahl.
Falls \(x^{p-1}\:mod\:p = 1\), ist \(p\) eine Primzahl oder \(p\) ist eine Carmichael-Zahl oder \(p\) ist zusammengesetzt. Falls \(p\) zusammengesetzt und keine Carmichael-Zahl ist, war die Wahrscheinlichkeit, ein solches \(x\) zu wählen, höchstens \(\frac{1}{2}\).
Der Fermat-Test kann offenbar in Abhängigkeit von \(p\) und \(x\) zwei verschiedene Ergebnisse liefern:
Falls der Test Ausgabe a. liefert, ist \(p\) mit absoluter Sicherheit zusammengesetzt und keine Primzahl.
Falls der Test hingegen Ausgabe b. liefert, haben wir zunächst keine Gewissheit: \(p\) kann dann eine Primzahl, eine Carmichael-Zahl oder eine zusammengesetzte (und keine Carmichael-)Zahl sein. Die Wahrscheinlichkeit für letzteres ist dabei höchstens \(\frac{1}{2}\).
Gäbe es keine Carmichael-Zahl, hätten wir damit einen sehr guten Primzahltest gefunden: Wir könnten den Test einfach mehrmals hintereinander ausführen - natürlich jedes Mal mit einem anderen \(x\). Wenn das Testergebnis jedes Mal b. lautet, können wir dadurch die Wahrscheinlichkeit, dass \(p\) tatsächlich eine zusammengesetzte Zahl ist, theoretisch beliebig minimieren. Indem man den Test k-mal durchführt, verringert sich die Wahrscheinlichkeit auf höchstens \(\frac{1}{2} \cdot \frac{1}{2} \cdot\:\dots\:\cdot\frac{1}{2} = \frac{1}{2^k}\).
Leider haben Alford, Granville und Pommerance (1994) gezeigt, dass es unendlich viele Carmichael-Zahlen gibt. Durch eine genauere Untersuchung dieser Zahlen kann man zwar zu einer Optimierung des Fermat-Tests gelangen. Wir belassen es bei der oben aufgeführten Beschreibung des Fermat-Tests und erwähnen stattdessen eine einfachere, aber auch eingeschränktere Lösung: Indem man eine Liste aller Carmichael-Zahlen bis zu einer gewissen Obergrenze anlegt und dann für den Fall b. prüft, ob die betrachtete Zahl \(p\) in dieser Liste vorkommt, erhält man einen effizienten und praxistauglichen Test. Die Liste der Carmichael-Zahlen bleibt dabei auch für große Zahlen noch überschaubar gering.