Mengen

Eigenschaften und Rechenregeln für Mengen

Zunächst wollen wir konkretisieren, was wir unter einer Menge verstehen. Wir verwenden hierfür die Definition von Georg Cantor (1845-1918). Cantor war ein berühmter deutscher Mathematiker und der Begründer der Mengenlehre.

Definition: Menge

Unter einer Menge verstehen wir jede Zusammenfassung \(M\) von bestimmten wohlunterschiedenen Objekten \(m\) unserer Anschauung oder unseres Denkens (welche die Elemente von \(M\) genannt werden) zu einem Ganzen.

Eine Menge fasst also Objekte zusammen, die jeweils klar voneinander unterscheidbar sind. Diese Objekte nennen wir die Elemente der Menge. Es wird zunächst keine Aussage darüber getroffen, welcher Art die Elemente einer Menge sein müssen. Es kann sich um Objekte der realen Welt, z.B. eine Gruppe von Personen handeln, aber auch um mathematische Konstrukte, wie z.B. die Menge der natürlichen Zahlen \(\mathbb{N}\). Mengen notiert man häufig mit Großbuchstaben, z.B. \(M\), während man für Objekte in der Regel Kleinbuchstaben verwendet, z.B. \(m\).

Um auszudrücken, dass ein Objekt \(m\) Element einer Menge \(M\) ist, schreiben wir \(m \in M\). Um auszudrücken, dass ein Objekt \(m\) nicht Element einer Menge \(M\) ist, schreiben wir \(m \notin M\).

Die leere Menge, also die Menge, die kein einziges Element besitzt, bezeichnen wir mit \(\emptyset\). Die Elemente einer Menge notiert man innerhalb geschweifter Klammern, den sogenannten Mengenklammern. Beispielsweise bezeichnet \(M := \{a, b, c\}\) eine Menge \(M\), die die drei Elemente \(a, b\) und \(c\) enthält. Es ist also \(a \in M\), \(b \in M\) und \(c \in M\).

Häufig möchte man zusätzlich ausdrücken, dass die Elemente einer Menge über eine bestimmte Eigenschaft \(e\) verfügen. Dieser Sachverhalt lässt sich notieren als \(M = \{m|m\) hat die Eigenschaft \(e\}\). In diesem Fall wäre \(M\) die Menge aller Elemente, die die Eigenschaft \(e\) haben. Die Angabe einer solchen Eigenschaft ist optional.

Beispiele: Mengen

1. \(\mathbb{N}\) ist die Menge der natürlichen Zahlen. Wir können dies schreiben als \(\mathbb{N} := \{1, 2, 3, 4, \dots\}\).
2. \(\mathbb{Z}\) ist die Menge der ganzen Zahlen. Wir können dies schreiben als \(\mathbb{Z} := \{\dots, -3, -2, -1, 0, 1, 2, 3, \dots\}\).
3. Sei \(M\) die Menge der Zahlen 1, 2, 3, 4. Dann können wir dies schreiben als \(M := \{1, 2, 3, 4\}\).
4. Sei \(P\) die Menge aller Personen mit blonden Haaren. Dann können wir dies schreiben als \(P := \{p|p\) hat blonde Haare\(\}\).
5. Sei \(U\) die Menge aller ungeraden Zahlen. Dann können wir dies schreiben als \(U := \{u|u\) ist eine ungerade Zahl\(\}\).

Häufig ist diese Schreibweise aber zu allgemein. Betrachtet man beispielsweise die Menge der Personen mit blonden Haaren, so stellt sich unweigerlich die Frage, aus welcher Gesamtmenge oder übergeordneten Gruppe von Personen diese ausgewählt werden. Betrachtet man alle Personen einer bestimmten Stadt? Oder alle Studenten eines Kurses? Oder die gesamte Weltbevölkerung? Ähnliches gilt z.B. für die oben definierte Menge \(U\). Aus welcher Grundmenge wählt man die ungeraden Zahlen als Elemente für \(U\) aus? Nur aus den natürlichen Zahlen \(\mathbb{N}\)? Oder aus den ganzen Zahlen \(\mathbb{Z}\)? Um dies zu präzisieren führen wir die Begriffe Teil- und Obermenge ein.

Definition: Teilmenge und Obermenge

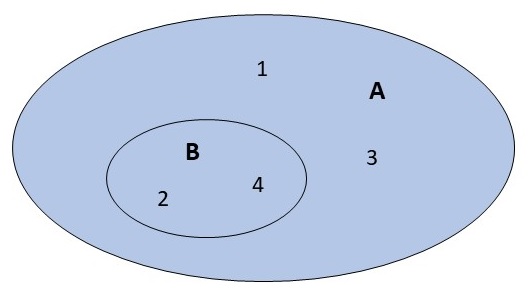
Eine Menge \(N\) heißt Teilmenge einer Menge \(M\), wenn jedes Element aus \(N\) auch in \(M\) liegt. Wir schreiben hierfür \(N \subseteq M\). Die Menge \(M\) heißt dann Obermenge von \(N\).

Beispiele: Teilmengen und Obermengen

1. Sei \(A := \{1, 2, 3, 4\}\) und sei \(B := \{2, 4\}\). Dann ist \(A\) eine Obermenge von \(B\) und \(B\) ist eine Teilmenge von \(A\). Es gilt also \(B \subseteq A\). Die folgende Abbildung illustriert diesen Zusammenhang.
   
2. Sei \(P\) die Menge aller Personen mit Wohnsitz in Berlin. Dann können wir die Menge aller Personen mit blonden Haaren in dieser Gruppe definieren als \(P' := \{p \in P|p\) hat blonde Haare\(\}\). \(P\) ist dann eine Obermenge von \(P'\) und \(P'\) ist eine Teilmenge von \(P\). Es gilt also \(P' \subseteq P\).
3. Wir definieren die Menge aller ungeraden natürlichen Zahlen als \(N' := \{n \in \mathbb{N}|n\) ist ungerade\(\}\). Dann ist \(\mathbb{N}\) eine Obermenge von \(N'\) und \(N'\) ist eine Teilmenge von \(\mathbb{N}\). Es gilt also \(N' \subseteq \mathbb{N}\).
4. Jede natürliche Zahl ist auch eine ganze Zahl und jede ganze Zahl ist auch eine reelle Zahl. Es gilt also \(\mathbb{N} \subseteq \mathbb{Z} \subseteq \mathbb{R}\).

Um deutlich auszudrücken, dass eine Menge \(N\) gerade eben keine Teilmenge einer Menge \(M\) ist, verwendet man das Teilmengen-Symbol in durchgestrichener Form und schreibt \(N \not \subseteq M\).

Definition: Gleichheit von Mengen

Zwei Mengen \(M\) und \(N\) sind gleich, wenn \(N \subseteq M\) und \(M \subseteq N\) gilt, wenn also alle Elemente von \(N\) auch in \(M\) liegen und umgekehrt.

Beispiel: Gleichheit von Mengen

Seien \(M := \{1, 2, 3\}\) und \(N := \{1, 2, 3\}\). Offenbar ist \(M \subseteq N\), denn alle Elemente von \(M\), also 1, 2 und 3, liegen auch in \(N\). Ebenso ist \(N \subseteq M\), denn alle Elemente von \(N\), also 1, 2 und 3, liegen auch in \(M\). Damit sind die Mengen \(M\) und \(N\) gleich, d.h., es ist \(M = N\). Genau wie in diesem Beispiel geht man übrigens in der Regel immer vor, wenn man zeigen möchte, dass zwei Mengen \(M\) und \(N\) gleich sind: Man zeigt zunächst, dass \(M\) eine Teilmenge von \(N\) ist. Anschließend zeigt man, dass auch \(N\) eine Telmenge von \(M\) ist. Daraus folgt dann die Gleichheit.

Als nächstes führen wir verschiedene Operationen (auch Verknüpfungen genannt) ein, die man auf Mengen durchführen kann.

Definition: Vereinigung von Mengen

Seien \(M\) und \(N\) Mengen. Dann definieren wir die Vereinigung von \(M\) und \(N\) als \(M \cup N := \{x|x \in M \lor x\in N\}\). Ausgesprochen wird dies "\(M\) vereinigt \(N\)".

Die Menge \(M \cup N\) besteht also aus allen Elementen, die in \(M\) oder in \(N\) (oder auch in beiden Mengen) vorkommen. Zu beachten ist dabei, dass Mengen generell niemals doppelte Elemente enthalten. D.h., auch ein Element, das in beiden Mengen \(M\) und \(N\) vorkommt, ist in \(M \cup N\) nur einmal enthalten.

Definition: Durchschnitt/Schnittmenge von Mengen

Seien \(M\) und \(N\) Mengen. Dann definieren wir den Durchschnitt (auch Schnittmenge genannt) von \(M\) und \(N\) als \(M \cap N := \{x|x \in M \land x \in N\}\). Ausgesprochen wird dies "\(M\) geschnitten \(N\)".

Definition: Differenz von Mengen

Seien \(M\) und \(N\) Mengen. Dann definieren wir die Differenz von \(M\) und \(N\) als \(M\backslash N := \{x|x \in M \land x \notin N\}\). Ausgesprochen wird dies "\(M\) ohne \(N\)".

Die Menge \(M \backslash N\) enthält also gerade diejenigen Elemente, die nur in \(M\), aber nicht in \(N\) vorkommen.

Beispiel: Vereinigung, Schnitt und Differenz von Mengen

Seien \(M := \{1, 2, 3, 4\}\) und \(N := \{3, 4, 5, 6\}\). Dann ist \[M \cup N = \{1, 2, 3, 4, 5, 6\}\] \[M \cap N = \{3, 4\}\] \[M \backslash N = \{1, 2\}\]

Die Verknüpfungen von Mengen lassen sich sehr gut durch sogenannte Venn-Diagramme veranschaulichen. Diese Mengendiagramme wurden nach dem englischen Mathematiker John Venn (1834-1923) benannt. Die nachstehende Abbildung veranschaulicht die verschiedenen Verknüpfungen anhand einer solchen grafischen Darstellung zweier Mengen \(A\) und \(B\). Der eingefärbte Bereich kennzeichnet jeweils das Ergebnis der Operation. Bei der Vereinigung erstreckt sich dieser über beide Kreise, denn die Vereinigung enthält ja gerade alle Elemente, die in \(A\) oder in \(B\) oder in beiden enthalten sind. Beim Durchschnitt ist der eingefärbte Bereich nur der mittlere Teil, in dem sich die beiden Kreise schneiden, denn der Durchschnitt enthält ja nur diejenigen Elemente, die sowohl in \(A\) als auch in \(B\) vorkommen. Bei der Differenz ist der gesamte Kreis von A mit Ausnahme desjenigen Bereichs eingefärbt, der von \(B\) überdeckt wird, denn die Differenz enthält ja gerade die Elemente, die nur in \(A\) aber nicht in \(B\) liegen.

Vereinigung (links), Durchschnitt (Mitte) und Differenz (rechts) von Mengen:

Definition: Disjunkt

Zwei Mengen \(M\) und \(N\) heißen disjunkt, wenn \(M \cap N = \emptyset\) gilt, die Schnittmenge also leer ist.

Zwei disjunkte Mengen haben kein einziges gemeinsames Element, das in beiden Mengen vorkommt.

Satz: Assoziativgesetze für Mengen

Seien \(L, M\) und \(N\) Mengen. Dann gelten die beiden folgenden Regeln: \[L \cup (M \cup N) = (L \cup M) \cup N\] \[L \cap (M \cap N) = (L \cap M) \cap N\]

Beweis:

Zunächst beweisen wir, dass \(L \cup (M \cup N) = (L \cup M) \cup N\) gilt. Hierzu orientieren wir uns an der Definition zur Gleichheit von Mengen: Wenn wir zeigen können, dass die Menge auf der linken Seite eine Teilmenge der Menge auf der rechten Seite ist und umgekehrt, dann folgt, dass die beiden Mengen gleich sind. Genauso wollen wr vorgehen:

Wir zeigen zunächst, dass \(L \cup (M \cup N) \subseteq (L \cup M) \cup N\) ist. Hierzu müssen wir zeigen, dass jedes Element aus \(L \cup (M \cup N)\) auch in \((L \cup M) \cup N\) liegt. Sei also \(x\) ein beliebiges Element dieser Menge, also \(x \in L \cup (M \cup N)\). Da \(x\) in der Vereinigung von \(L\) und \(M \cup N\) liegt, muss \(x\) in mindestens einer dieser Mengen liegen. Wir können demnach eine Fallunterscheidung durchführen. Falls \(x \in L\) ist, so ist auch \(x \in L \cup M\), und damit auch \(x \in (L \cup M) \cup N\). Falls \(x \in M \cup N\) ist, so liegt \(x\) in \(M\) oder in \(N\) oder in beiden. Falls \(x \in M\) ist, so ist auch \(x \in (L \cup M)\), und damit auch \(x \in (L \cup M) \cup N\). Falls \(x \in N\), so ist entsprechend \(x \in (L \cup M) \cup N.\) Damit folgt \(L \cup (M \cup N) \subseteq (L \cup M) \cup N\).

Analog zeigt man, dass \(L \cup (M \cup N) \supseteq (L \cup M) \cup N\). Daraus folgt dann insgesamt der erste Teil der Behauptung, nämlich \(L \cup (M \cup N) = (L \cup M) \cup N\).

Den zweiten Teil der Behauptung zeigt man auf ähnliche Weise:

Sei \(x \in L \cap (M \cap N)\). Dann liegt \(x\) sowohl in \(L\) als auch in \(M \cap N\). Aus \(x \in M \cap N\) folgt weiter, dass \(x\) sowohl in \(M\) als auch in \(N\) liegt. Damit folgt weiter, dass \(x\) auch in \(L \cap M\) und damit in \((L \cap M) \cap N\) liegt. Somit folgt insgesamt \(L \cap (M \cap N) \subseteq (L \cap M) \cap N\).

Analog zeigt man, dass \(L \cap (M \cap N) \supseteq (L \cap M) \cap N\). Daraus folgt dann insgesamt der zweite Teil der Behauptung, nämlich \(L \cap (M \cap N) = (L \cap M) \cap N\). \(\square\)

Beispiel: Assoziativgesetze für Mengen

Seien \(L := \{1, 2, 3\}, M := \{3, 4\}\) und \(N := \{3, 5\}\). Dann ist \[L \cup (M \cup N) = \{1, 2, 3\} \cup (\{3, 4\} \cup \{3, 5\})\] \[= \{1, 2, 3\} \cup \{3, 4, 5\}\] \[= \{1, 2, 3, 4, 5\}\] \[= \{1, 2, 3, 4\} \cup \{3, 5\}\] \[= (\{1, 2, 3\} \cup \{3, 4\}) \cup \{3, 5\}\] \[= (L \cup M) \cup N\]

und \[L \cap (M \cap N) = \{1, 2, 3\} \cap (\{3, 4\} \cap \{3, 5\})\] \[= \{1, 2, 3\} \cap \{3\}\] \[= \{3\}\] \[= \{3\} \cap \{3, 5\}\] \[= (\{1, 2, 3\} \cap \{3, 4\}) \cap \{3, 5\}\] \[= (L \cap M) \cap N\]

Satz: Distributivgesetze für Mengen

Seien \(L, M\) und \(N\) Mengen. Dann gelten die beiden folgenden Regeln: \[L \cup (M \cap N) = (L \cup M) \cap (L \cup N)\] \[L \cap (M \cup N) = (L \cap M) \cup (L \cap N)\]

Die folgenden wichtigen Regeln stammen vom britischen Mathematiker Augustus de Morgan (1806-1871) und wurden auch nach ihm benannt.

Satz: Regeln von de Morgan

Seien \(L, M\) und \(N\) Mengen. Dann gelten die beiden folgenden Regeln: \[L \backslash (M \cap N) = (L \backslash M) \cup (L \backslash N)\] \[L \backslash (M \cup N) = (L \backslash M) \cap (L \backslash N)\]

Beweis:

Wir beweisen zunächst die erste Regel von de Morgan und gehen dabei analog zu den vorherigen Beweisen vor.

Sei \(x \in L \backslash (M \cap N)\). Dann ist \(x \in L\) und \(x \not \in M \cap N\). Letzteres bedeutet, dass \(x\) entweder nur in einer der beiden Mengen \(M, N\) oder in keiner davon enthalten ist. Falls \(x \in M \land x \not \in N\) ist, gilt wegen \(x \in L\), dass \(x \in L \backslash N\) und damit \(x \in (L \backslash M) \cup (L \backslash N)\) ist. Falls \(x \not \in M \land x \in N\) ist, gilt entsprechend \(x \in L \backslash M\) und damit \(x \in (L \backslash M) \cup (L \backslash N)\). Falls \(x \not \in M \land x \not \in N\) ist, gilt sogar \(x \in L \backslash M\) und \(x \in L \backslash N\) und damit insbesondere \(x \in (L \backslash M) \cup (L \backslash N)\). Damit folgt \(L \backslash (M \cap N) \subseteq (L \backslash M) \cup (L \backslash N)\).

Sei \(x \in (L \backslash M) \cup (L \backslash N)\). Dann ist \(x \in L \backslash M\) oder \(x \in L \backslash N\) oder \(x\) liegt in beiden Mengen. Falls \(x \in L \backslash M\) ist, so ist \(x \in L\) und \(x \not \in M\). Daraus folgt, dass \(x \not \in M \cap N\) ist, und damit \(x \in L \backslash (M \cap N)\). Falls \(x \in L \backslash N\) ist, so ist \(x \in L\) und \(x \not \in N\). Daraus folgt entsprechend, dass \(x \not \in M \cap N\) ist, und damit \(x \in L \backslash (M \cap N)\). Damit folgt \(L \backslash (M \cap N) \supseteq (L \backslash M) \cup (L \backslash N)\) und damit die erste Regel von de Morgan.

Die zweite Regel von de Morgan wird auf analoge Weise bewiesen. Damit folgt insgesamt die Behauptung. \(\square\)

Der folgende Satz zeigt einige weitere interessante Eigenschaften von Teilmengen bezüglich Vereinigung und Schnitt. Der Beweis dieses Satzes soll gleichzeitig die Beweistechnik durch Ringschluss illustrieren.

Satz: Eigenschaften von Teilmengen bezüglich Vereinigung und Schnitt

Seien \(M\) und \(N\) Mengen. Dann sind folgende Aussagen äquivalent:

1. \(N \subseteq M\)
2. \(M \cap N = N\)
3. \(M \cup N = M\)

Beweis:

(1) \(\Rightarrow\) (2)

Es gelte \(N \subseteq M\). Für alle \(x \in N\) gilt somit auch \(x \in M\). Nach Definition der Schnittmenge ist \(M \cap N := \{x|x \in M \land x \in N\}\). Für alle \(x \in N\) ist folglich \(x \in M \cap N\) und damit \(N \subseteq M \cap N\).

Für alle \(x \in M \cap N\) ist per Definition \(x \in M\) und insbesondere auch \(x \in N\). Damit folgt \(M \cap N \subseteq N\).

Damit folgt insgesamt \(M \cap N = N\).

(2) \(\Rightarrow\) (3)

Es gelte \(M \cap N = N\). Nach Definition der Vereinigung ist \(M \cup N := \{x|x \in M \lor x \in N\}\). Für alle \(x \in M\) ist somit \(x \in M \cup N\) und damit \(M \subseteq M \cup N\).

Für alle \(x \in M \cup N\) gilt, dass \(x \in M\) oder \(x \in N\). Für alle \(x \in N\) ist wegen \(M \cap N = N\) auch \(x \in M \cap N\) und damit \(x \in M\). Damit folgt \(M \cup N \subseteq M\).

Damit folgt insgesamt \(M \cup N = M\).

(3) \(\Rightarrow\) (1)

Es gelte \(M \cup N = M\). Angenommen, es wäre \(N \not \subseteq M\). Dann gibt es \(x \in N\) mit \(x \not \in M\). Daraus folgt, dass es \(x \in M \cup N\) gibt mit \(x \not \in M\). Dies führt zu einem Widerspruch, denn dann kann nicht \(M \cup N = M\) gelten. Somit ist die Annahme \(N \not \subseteq M\) falsch. Es folgt demnach \(N \subseteq M\). \(\square\)

Definition: Mächtigkeit/Kardinalität

Sei \(M\) eine Menge. Dann definieren wir die Mächtigkeit (auch Kardinalität genannt) einer Menge als \[|M| := \left\{\begin{array}{ll}\text{ n, falls } n \in \mathbb{N} \cup \{0\} \text{ die Anzahl der Elemente in } M \text{ ist } \\ \infty, \text{ falls } M \text{ unendlich viele Elemente besitzt}\end{array}\right.\]

\(\infty\) ist dabei das mathematische Symbol für unendlich.

Beispiele: Mächtigkeit/Kardinalität

1. Sei \(M_1 := \{a, b, c, d\}\). Dann ist \(|M_1| = 4\).
2. Sei \(M_2 := \{1, 2, 3, 4, 5, 6, 7, 8\}\) und sei \({M'}_2 \subseteq M_2\) mit \({M'}_2 := \{m \in M_2|m\) ist gerade\(\} = \{2, 4, 5, 8\}\). Dann ist \(|M_2| = 8\) und \(|{M'}_2| = 4\).
3. Sei \(M_3 := \mathbb{N}\). Dann ist \(|M_3| = \infty\).

Definition: Potenzmenge

Sei \(M\) eine Menge. Dann definieren wir die Potenzmenge von \(M\) als die Menge aller möglichen Teilmengen von \(M\) und bezeichnen sie mit \(P(M)\).

Es ist zu beachten, dass die leere Menge \(\emptyset\) stets eine mögliche Teilmenge jeder anderen Menge ist! Somit ist \(\emptyset\) immer in jeder Potenzmenge enthalten.

Beispiele: Potenzmenge

1. Sei \(M_1 := \{a, b, c, d\}\). Dann ist \[P(M_1) = \{\emptyset, \{a\}, \{b\}, \{c\}, \{d\}, \{a, b\}, \{a, c\}, \{a, d\}, \{b, c\}, \{b, d\}, \{c, d\}, \{a, b, c\}, \{a, b, d\}, \{a, c, d\}, \{b, c, d\}, \{a, b, c, d\}\}\]
2. Sei \(M_2 := \{1, 2, 3\}\). Dann ist \[P(M_2) = \{\emptyset, \{1\}, \{2\}, \{3\}, \{1, 2\}, \{1, 3\}, \{2, 3\}, \{1, 2, 3\}\}\]

Die Potenzmenge einer endlichen Menge ist stets endlich, die Potenzmenge einer unendlichen Menge ist unendlich.

Satz: Mächtigkeit der Potenzmenge

Sei \(M\) eine endliche Menge mit \(|M| = n \in \mathbb{N}_0\). Dann gilt \(|P(M)| = 2^n\).

Beweis:

Wir beweisen die Aussage dieses Satzes mit vollständiger Induktion:

Induktionsanfang: Sei \(n = 0\). Dann ist \(M\) die leere Menge. Die Potenzmenge der leeren Menge hat nur ein einziges Element, nämlich die leere Menge selbst. Es ist also \(|P(M)| = 1 = 2^0\) und damit gilt der Induktionsanfang.

Induktionsschritt: Sei nun \(n \geq 0\). Es gelte \(|P(M)| = 2^n\) für jede endliche Menge \(M\) mit \(n\) Elementen. Wir müssen zeigen, dass daraus \(|P(M')| = 2^{n+1}\) für jede endliche Menge \(M'\) mit \(n + 1\) Elementen folgt.

Sei \(M'\) eine Menge mit \(n + 1\) Elementen, also \(M' := \{a_1, \dots, a_{(n+1)}\}\). Wir untersuchen, wie viele verschiedene Teilmengen \(M'\) besitzt. Sei hierzu \(L'\) eine beliebige Teilmenge von \(M'\), also \(L' \subseteq M'\). Dann gibt es genau zwei Möglichkeiten:

1. Möglichkeit: \(a_{(n+1)} \in L'\)
2. Möglichkeit: \(a_{(n+1)} \not \in L'\)

Zu 1.: Wenn \(a_{n+1} \in L'\) ist, so ist \(L'\) von der Form \(L' = L \cup \{a_{n+1}\}\) mit \(L \subseteq M := \{a_1, \dots, a_n\}\). Wir wissen, dass es \(2^n\) verschiedene Teilmengen von \(M\) gibt, denn wegen \(|M| = n\) ist \(|P(M)| = 2^n\). Da \(L\) eine Teilmenge von \(M\) ist, gibt es deshalb \(2^n\) Möglichkeiten, wie \(L\) aussehen kann. Somit existieren \(2^n\) Möglichkeiten, wie \(L'\) aussehen kann, und folglich gibt es \(2^n\) Teilmengen von \(M'\), die \(a_{n+1}\) enthalten.

Zu 2.: Wenn \(a_{n+1} \not \in L'\) ist, so ist \(L'\) eine Teilmenge von \(M := \{a_1, \dots, a_n\}\). Wir wissen, dass es \(2^n\) verschiedene Teilmengen von \(M\) gibt, denn \(|P(M)| = 2^n\). Folglich gibt es \(2^n\) verschiedene Möglichkeiten für \(L'\) und damit \(2^n\) Teilmengen von \(M'\), die \(a_{n+1}\) nicht enthalten.

Da es keine weiteren Möglichkeiten gibt, existieren somit genau \(2^n\) Teilmengen von \(M'\) die \(a_{n+1}\) enthalten, und \(2^n\) Teilmengen von \(M'\), die \(a_{n+1}\) nicht enthalten. \(M'\) hat damit insgesamt \(2^n + 2^n = 2 \cdot 2^n = 2^{n+1}\) Teilmengen und es folgt \(|P(M')| = 2^{n+1}\). \(\square\)

Definition: Kartesisches Produkt

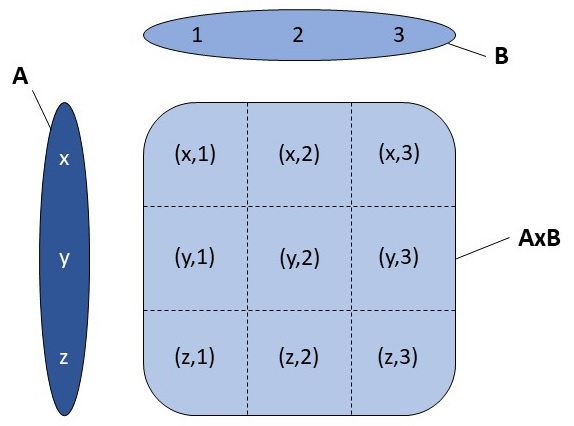
Seien \(M\) und \(N\) nichtleere Mengen. Dann ist das kartesische Produkt von \(M\) und \(N\) definiert als \(M \times N := \{(m, n)|m \in M, n \in N\}\). Dabei wird \(M \times N\) ausgesprochen als "\(M\) kreuz \(N\)". Die durch \(M \times N\) definierte Menge bezeichnet man auch als Produktmenge.

Die \((m, n) \in M \times N\) nennen wir geordnete Paare. Zwei geordnete Paare \((m_1, n_1)\) und \((m_2, n_2)\) sind genau gleich, wenn \(m_1 = m_2\) und \(n_1 = n_2\) gilt.

Beispiele: Kartesisches Produkt

1. Sei \(A := \{x, y, z\}\) und \(B := \{1, 2, 3\}\). Die Produktmenge des kartesischen Produkts von \(A\) und \(B\) ist \(A \times B = \{(x, 1), (x, 2), (x, 3), (y, 1), (y, 2), (y, 3), (z, 1), (z, 2), (z, 3)\}\). Die folgende Abbildung veranschaulicht die Bildung der Produktmenge noch einmal grafisch.
   
2. Wir können auch das kartesische Produkt von unendlichen Mengen betrachten. Beispielsweise ist \(\mathbb{N} \times \mathbb{N}\) das kartesische Produkt der natürlichen Zahlen. Die Produktmenge ist dann die unendliche Menge aller möglichen geordneten Paare mit Elementen aus \(\mathbb{N}\), also \(\mathbb{N} \times \mathbb{N} = \{(1, 1), (1, 2), (1, 3), \dots, (2, 1), (2, 2), (2, 3), \dots\}\).