Mathematik Grundlagen I

>> Wissensdatenbank / Mathematik / Mathematik Grundlagen I

Abbildungen

Hier wird beschrieben, was man unter Abbildungen (auch Funktionen genannt) versteht und welche grundlegenden Eigenschaften diese haben. Abbildungen spielen in vielen Bereichen der Mathematik eine außerordentlich wichtige Rolle. Sie besitzen Ähnlichkeiten zu den aus der Informatik bekannten Funktionen, die man in einer Programmier- oder Skriptsprache aufrufen kann: Sie erwarten eine bestimmte Anzahl von Parametern und liefern einen Rückgabewert zurück.

Abbildungen und Graphen

Zunächst soll definiert werden, was man allgemein in der Mathematik unter einer Abbildung versteht.

Definition: Abbildung

Seien \(A\) und \(B\) nichtleere Mengen. Dann ist eine Abbildung (auch Funktion genannt) \(f\) mit Definitionsbereich \(A\) und Wertebereich \(B\) eine Vorschrift, die jedem Element aus \(A\) in eindeutiger Weise ein Element aus \(B\) zuordnet. Wir schreiben hierfür \(f : A \rightarrow B\) und sagen hierfür "\(f\) ist eine Abbildung von \(A\) nach \(B\) ".

Häufig schreibt man statt \(f : A \rightarrow B\) auch einfach nur \(f\), wenn \(A\) und \(B\) aus dem Kontext ersichtlich sind.

Ist ein \(x \in A\) gegeben, so nennt man das Element aus \(B\), das durch die Zuordnungsvorschrift eindeutig bestimmt ist, das Bild (oder den Funktionswert) von \(f\) an der Stelle \(x\). Man schreibt hierfür \(f(x)\). Das \(x\) bezeichnet man dann auch als Argument oder Eingabewert der Funktion \(f\). Es gilt zu beachten, dass wir an dieser Stelle aufgrund der Eindeutigkeit von "dem" Bild der Funktion \(f\) an der Stelle \(x\) sprechen dürfen.

Wenn \(f(x) = y\) ist, so wird \(x\) ein Urbild von \(y\) unter \(f\) genannt. Es gilt zu beachten, dass ein Urbild (im Gegensatz zum Bild) nicht eindeutig sein muss (denn es könnte durchaus verschiedene \(x_1, x_2\) geben, die auf den gleichen Funktionswert \(y\) abbilden, also \(f(x_1) = y = f(x_2)\) mit \(x_1 \not = x_2\)). Deshalb sprechen wir von "einem" Urbild.

Die Menge \(f(A) := \{y \in B|\exists\:x \in A : f(x) = y\} \subseteq B\) wird das Bild (oder die Bildmenge) von \(f\) genannt. Es ist zu beachten, dass (abhängig von der betrachteten Funktion) \(f(A) \not = B\) sein kann, da nicht jedes Element aus \(B\) ein Urbild besitzen muss. Funktionen, für die \(f(A) = B\) gilt, haben einen besonderen Namen.

Zwei Abbildungen \(f : A \rightarrow B\) und \(g : C \rightarrow D\) heißen gleich, wenn \(A = C\) und \(B = D\) gilt und wenn jedem Element aus \(A\) (bzw. \(C\)) durch \(f\) und \(g\) jeweils dasselbe Element in \(B\) (bzw. \(D\)) zugeordnet wird.

Beispiel: Abbildungen

Seien \(A := \{1, 2, 3\}\) und \(B := \{4, 5, 6\}\). Wir können eine Abbildung \(f : A \rightarrow B\) definieren, indem wir für jedes Argument explizit den Funktionswert definieren, z.B. \(f(1) := 4, f(2) := 5\) und \(f(3) := 6\). Dies ist jedoch nur für Mengen mit wenigen Elementen sinnvoll möglich. Für gewöhnlich definiert man daher eine Abbildung eher durch die Angabe einer Berechnungs- oder Zuordnungsvorschrift. Die vorige Funktion \(f\) könnten wir beispielsweise ebenso gut definieren als \(f(x) := x + 3\) für \(x \in \{1, 2, 3\}\).

Das Quadrat von reellen Zahlen können wir als Zweierpotenz-Funktion wie folgt definieren: \(f : \mathbb{R} \rightarrow \mathbb{R}_+\) mit \(f(x) := x^2\). Dann ist beispielsweise \(f(2) = 4\) und \(f(5) = 25\).

Eine sehr wichtige Funktion ist die sogenannte Identität oder Identitätsfunktion \(id\). Für eine Menge \(A\) ist diese Abbildung definiert als \(id_A : A \rightarrow A\) mit \(id_A(x) := x\). Mit \(A := \mathbb{R}\) ist dann z.B. \(id_\mathbb{R}(2) = 2\) und \(id_\mathbb{R}(42) = 42\).

Ebenfalls wichtig ist die konstante Funktion \(const\). Für eine Menge \(A\) und ein Element \(c \in A\) ist diese definiert als \(const_c : A \rightarrow A\) mit \(const_c(x) := c\). Mit \(A := \mathbb{R}\) und \(c := 7\) ist dann z.B. \(const_7(3) = 7\) und \(const_7(32) = 7\).

Ein weiteres populäres Beispiel für eine Abbildung ist die Wurzelfunktion \(\sqrt{\:\:}\). Diese ist definiert als \(\sqrt{\:\:} : \mathbb{R}_+ \rightarrow \mathbb{R}_+\) mit \(\sqrt{\:}(x) := \sqrt{x}\). Mit dieser Definition ist z.B. \(\sqrt{9} = 3\) und \(\sqrt{49} = 7\).

Eie weitere wichtige Funktion ist die sogenannte Betragsfunktion \(||\). Diese ist definiert als \(|| : \mathbb{R} \rightarrow \mathbb{R}_+\) mit \[||\:(x) := |x| := \left\{\begin{array}{ll}x \text{, falls } x \geq 0\\ -x \text{, falls } x \lt 0\end{array}\right.\] Es ist beispielsweise \(|5| = 5, |-32,4| = 32,4\) und \(|0| = 0\).

Um Abbildungen bzw. deren Funktionswerte zu veranschaulichen, kann man sogenannte Graphen verwenden.

Definition: Graph einer Abbildung

Seien \(A\) und \(B\) Mengen und sei \(f : A \rightarrow B\) eine Abbildung von \(A\) nach \(B\). Die Menge \(G(f) := \{(x, f(x)) | x \in A\}\) nennt man den Graphen von \(f\).

Um den Graphen einer Funktion \(f : A \rightarrow B\) grafisch darzustellen, geht man wie folgt vor:
Man zeichnet ein Koordinatensystem mit einer horizontalen x-Achse und einer dazu senkrechten y-Achse. Dort trägt man alle Punkte \((x, f(x))\) mit \(x \in A\) ein. Die folgenden Abbildungen skizzieren die Graphen für die Funktionen aus den oben aufgeführten Beispielen.

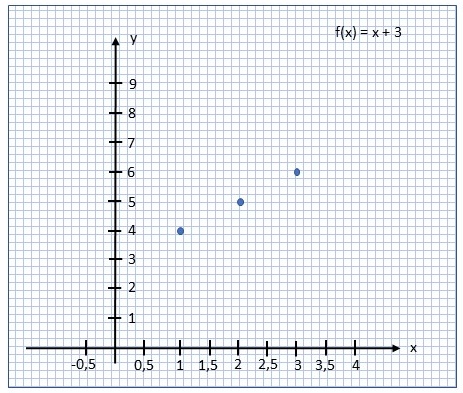
Graph der Funktion \(f : \{1, 2, 3\} \rightarrow \{4, 5, 6\}\) mit \(f(x) := x + 3\)

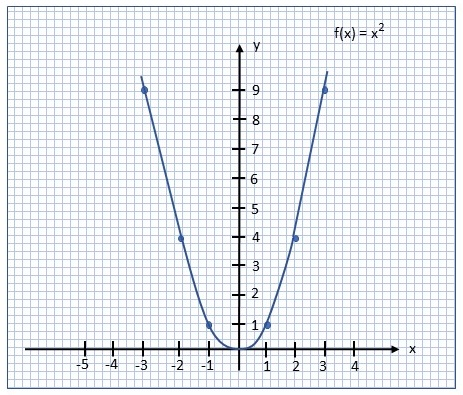
Graph der Zweierpotenz \(f : \mathbb{R} \rightarrow \mathbb{R}_+, f(x) := x^2\)

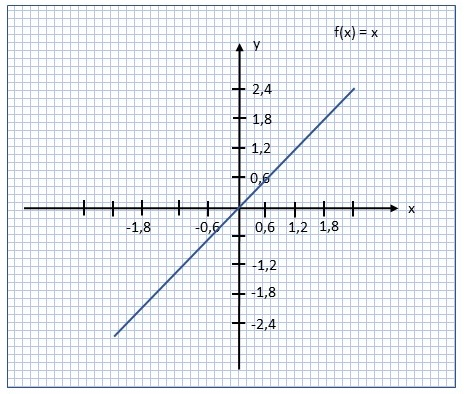
Graph der Identitätsfunktion \(id_\mathbb{R} : \mathbb{R} \rightarrow \mathbb{R}, id_\mathbb{R}(x) := x\)

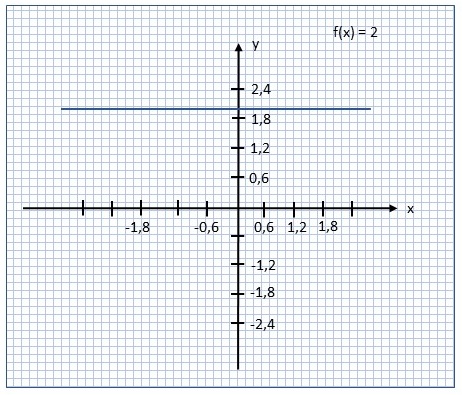
Graph der konstanten Funktion \(const_2 : \mathbb{R} \rightarrow \mathbb{R}, const_2(x) := 2\)

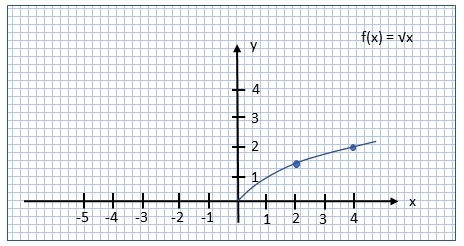
Graph der Wurzelfunktion \(\sqrt{\:\:} : \mathbb{R}_+ \rightarrow \mathbb{R}_+, \sqrt{\:}(x) := \sqrt{x}\)

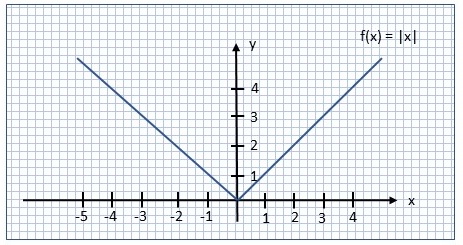
Graph der Betragsfunktion \(\|\| : \mathbb{R} \rightarrow \mathbb{R}_+, \|\|\:(x) := \left\{\begin{array}{ll}x \text{, falls } x \geq 0\\ -x \text{, falls } x \lt 0\end{array}\right.\)

Gelegentlich möchte man mehrere Funktionen hintereinander ausführen, z.B. aus einer Zahl \(x\) zuerst die Wurzel ziehen und anschließend einen Wert \(m\) hinzuaddieren. Dieser Sachverhalt lässt sich für Funktionen ganz allgemein definieren.

Definition: Komposition

Seien \(A, B, C\) und \(D\) nichtleere Mengen und seien \(f : A \rightarrow B\) und \(g : C \rightarrow D\) zwei Abbildungen. Weiterhin gelte \(f(x) \in C\) für alle \(x \in A\). Dann ist die Komposition (auch Verkettung oder Hintereinanderausführung) der Funktionen \(f\) und \(g\) definiert durch \[g \circ f : A \rightarrow D, (g \circ f)(x) := g(f(x))\] Man spricht \(g \circ f\) aus als "\(g\) komponiert (mit) \(f\)" oder "\(g\) nach \(f\)".

Beispiel: Komposition

Sei \(f : \mathbb{R} \rightarrow \mathbb{R}\) mit \(f(x) := x + 3\) und \(g : \mathbb{R} \rightarrow \mathbb{R}\) mit \(g(x) := x^2\).
Dann ist die Komposition von \(f\) und \(g\) gegeben durch \(g \circ f : \mathbb{R} \rightarrow \mathbb{R}\) mit \((g \circ f)(x) := (x + 3)^2\).

Sei \(f : \mathbb{N} \rightarrow \mathbb{N}\) mit \(f(x) := x + 5\) und \(g : \mathbb{N} \rightarrow \mathbb{N}\) mit \(g(x) := 3x\).
Dann ist die Komposition von \(f\) und \(g\) gegeben durch \(g \circ f : \mathbb{N} \rightarrow \mathbb{N}\) mit \((g \circ f)(x) := 3(x + 5)\).

Wir betrachten die Betragsfunktion \(|| : \mathbb{R} \rightarrow \mathbb{R}_+\) und die Wurzelfunktion \(\sqrt{\:} : \mathbb{R}_+ \rightarrow \mathbb{R}_+\). Wegen \(|x| \geq 0\) für alle \(x \in \mathbb{R}\) können wir die Komposition von \(||\) und \(\sqrt{\:}\) bilden als \(\sqrt{\:} \circ || : \mathbb{R} \rightarrow \mathbb{R}_+\) mit \((\sqrt{\:} \circ ||)(x) := \sqrt{|x|}\).

Satz: Assoziativität der Komposition

Seien \(A, B, C\) und \(D\) Mengen und seien \(f : A \rightarrow B, g : B \rightarrow C\) und \(h : C \rightarrow D\) Abbildungen. Die Komposition von Abbildungen ist assoziativ, d.h. es gilt \(h \circ (g \circ f) = (h \circ g) \circ f\).

Beweis:

Zunächst überlegt man sich, dass die Kompositionen auf beiden Seiten des Gleichheitszeichens tatsächlich gültig sind und den gleichen Definitions- und Wertebereich haben:

\(f\) ist eine Abbildung von \(A\) nach \(B\) und \(g\) ist eine Abbildung von \(B\) nach \(C\). Damit ist \(g \circ f\) definiert und eine Abbildung von \(A\) nach \(C\). \(h\) ist eine Abbildung von \(C\) nach \(D\). Damit ist weiterhin \(h \circ (g \circ f)\) definiert und insgesamt eine Abbildung von \(A\) nach \(D\).

\(g\) ist eine Abbildung von \(B\) nach \(C\) und \(h\) ist eine Abbildung von \(C\) nach \(D\). Damit ist \(h \circ g\) definiert und eine Abbildung von \(B\) nach \(D\). \(f\) ist eine Abbildung von \(A\) nach \(B\). Damit ist weiterhin \((h \circ g) \circ f\) definiert und insgesamt eine Abbildung von \(A\) nach \(D\).

Beide Kompositionen sind somit gültig und haben jeweils den gleichen Definitions- und Wertebereich. Es bleibt zu zeigen, dass die Abbildungen tatsächlich gleich sind:

Wir definieren \(h_g := h \circ g\) und \(g_f := g \circ f\). Für alle \(a \in A\) gilt dann \[(h \circ (g \circ f))(a) = (h \circ g_f)(a)\] \[= h(g_f(a))\] \[= h((g \circ f)(a))\] \[= h(g(f(a)))\] sowie \[((h \circ g) \circ f)(a) = (h_g \circ f)(a)\] \[= h_g(f(a))\] \[= (h \circ g)(f(a))\] \[= h(g(f(a)))\] Damit folgt \((h \circ (g \circ f))(a) = ((h \circ g) \circ f)(a)\) für alle \(a \in A\) und somit die Behauptung \(h \circ (g \circ f) = (h \circ g) \circ f\). \(\square\)