Abbildungen

Besondere Eigenschaften von Abbildungen

Es gibt bestimmte Eigenschaften, die manche Abbildungen besonders auszeichnen. Im Folgenden wollen wir die wichtigsten davon kurz vorstellen.

Definition: Injektivität

Sei \(f : A \rightarrow B\) eine Abbildung. \(f\) heißt injektiv, wenn für alle \(a, a' \in A\) gilt: \[f(a) = f(a') \Rightarrow a = a'\] Mit anderen Worten: Eine Funktion heißt injektiv, wenn jedes Element des Wertebereichs \(B\) höchstens ein Urbild hat, d.h. wenn es keine zwei verschiedenen Eingabewerte gibt, die auf den gleichen Funktionswert abbilden.

Die folgende Abbildung veranschaulicht das Prinzip der Injektivität grafisch.

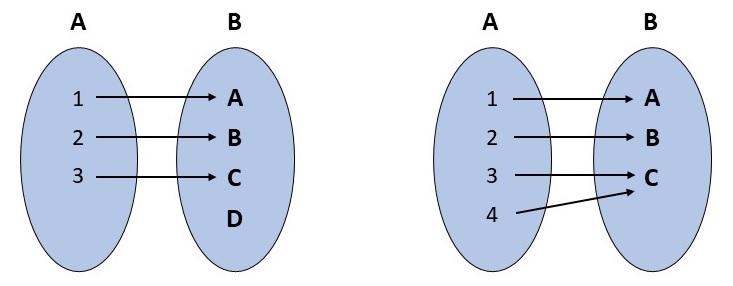
Links: Bei einer injektiven Abbildung hat jedes Element des Wertebereichs \(B\) höchstens ein Urbild in \(A\).
Rechts: Wenn ein Element mehrere mögliche Urbilder hat, ist die Funktion nicht injektiv.

Beispiel: Injektivität

1. Die Funktion \(f : \mathbb{R} \rightarrow \mathbb{R}_+\) mit \(f(x) := x^2\) ist nicht injektiv, denn es ist z.B. \(f(-1) = 1 = f(1)\).


2. Wenn wir hingegen den Definitionsbereich einschränken und die Funktion \(f : \mathbb{R}_+ \rightarrow \mathbb{R}_+\) mit \(f(x) := x^2\) betrachten, dann ist \(f\) injektiv, denn für \(a, a' \in \mathbb{R}_+\) mit \(f(a) = a^2 = f(a') = a'^2\) folgt \(a = a'\) wegen \(a, a' \geq 0\).


3. Die Funktion \(f : \mathbb{R} \rightarrow \mathbb{R}\) mit \(f(x) := x + 1\) ist injektiv, denn für \(a, a' \in \mathbb{R}\) mit \(f(a) = a + 1 = f(a') = a' + 1\) folgt \(a = a'\).


4. Die Funktion \(f : \mathbb{N} \rightarrow \mathbb{N}\) mit \(f(x) := 2x\) ist injektiv, denn für \(a, a' \in \mathbb{N}\) mit \(f(a) = 2a = f(a') = 2a'\) folgt \(a = a'\).

Definition: Surjektivität

Sei \(f : A \rightarrow B\) eine Abbildung. \(f\) heißt surjektiv, wenn es für jedes \(b \in B\) ein \(a \in A\) gibt mit \(f(a) = b\).

Mit anderen Worten: Eine Funktion heißt surjektiv, wenn es zu jedem Element des Wertebereichs \(B\) mindestens ein Urbild gibt. Für eine surjektive Funktion \(f : A \rightarrow B\) gilt also gerade \(f(A) = B\).

Die folgende Abbildung veranschaulicht das Prinzip der Surjektivität grafisch.

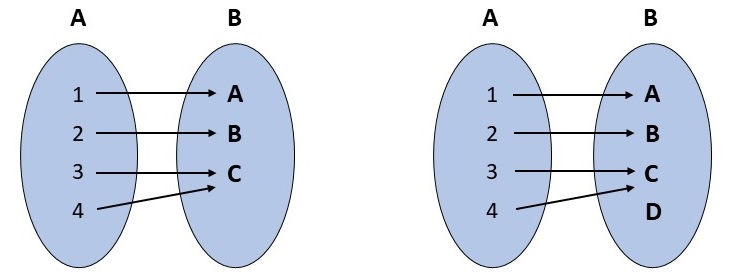
Links: Bei einer surjektiven Abbildung hat jedes Element des Wertebereichs \(B\) mindestens ein Urbild in \(A\).
Rechts: Wenn es Elemente im Wertebereich gibt, für die kein Urbild existiert, dann ist die Funktion nicht surjektiv.

Beispiel: Surjektivität

1. Die Funktion \(f : \mathbb{N} \rightarrow \mathbb{N}\) mit \(f(x) := 2x\) ist nicht surjektiv, denn das Bild von \(f\) sind die geraden natürlichen Zahlen. Die ungeraden natürlichen Zahlen besitzen somit keine Urbilder unter \(f\).


2. Die Funktion \(f : \mathbb{R} \rightarrow \mathbb{R}\) mit \(f(x) := x + 1\) ist surjektiv, denn zu jedem \(b \in \mathbb{R}\) existiert ein Urbild, nämlich \(b - 1 \in \mathbb{R}\): Es ist \(f(b - 1) = (b - 1) + 1 = b\).


3. Die Identitätsfunktion \(id_\mathbb{R} : \mathbb{R} \rightarrow \mathbb{R}\) mit \(id_\mathbb{R}(x) := x\) ist surjektiv, denn zu jedem \(b \in \mathbb{R}\) ist das Urbild gerade \(b\) mit \(id_\mathbb{R}(b) = b\).

Definition: Bijektivität

Sei \(f : A \rightarrow B\) eine Abbildung. \(f\) heißt bijektiv, wenn \(f\) injektiv und surjektiv ist.

Mit anderen Worten: Eine Funktion heißt bijektiv, wenn jedes Element des Wertebereichs \(B\) genau ein Urbild hat.

Die nachstehende Abbildung veranschaulicht das Prinzip der Bijektivität grafisch. Bijektive Abbildungen spielen in vielen Bereichen der Mathematik eine außerordentlich wichtige Rolle, wie wir im Folgenden sehen werden.

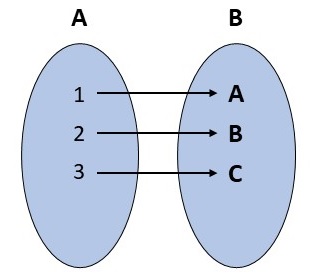
Beispiel: Bijektivität

1. Die Abbildung \(f : \mathbb{R} \rightarrow \mathbb{R}\) mit \(f(x) := x + 1\) ist bijektiv, denn sie ist injektiv und surjektiv.


2. Die Abbildung \(f : \mathbb{R} \rightarrow \mathbb{R}\) mit \(f(x) := x^2\) ist nicht bijektiv, denn sie ist weder injektiv noch surjektiv.


3. Die Abbildung \(f : \mathbb{N} \rightarrow \mathbb{N}\) mit \(f(x) := 2x\) ist nicht bijektiv, denn sie ist zwar injektiv aber nicht surjektiv.

Definition: Invertierbare Abbildung

Sei \(f : A \rightarrow B\) eine Abbildung. \(f\) heißt invertierbar (oder eine invertierbare Abbildung), wenn es eine Abbildung \(g : B \rightarrow A\) gibt mit \(g \circ f = id_A\) und \(f \circ g = id_B\).

Insbesondere gilt somit für eine invertierbare Funktion \(f\), dass \((g \circ f)(a) = a\) und \((f \circ g)(b) = b\) für alle \(a \in A\) und \(b \in B\).

Beispiel: Invertierbare Abbildungen

Sei \(A := \{1, 2, 3\}\) und \(B := \{4, 5, 6\}\). Sei die Abbildung \(f : A \rightarrow B\) definiert durch \(f(a) := a + 3\) für alle \(a \in A\). Dann ist \(f\) invertierbar, denn es gibt eine Abbildung \(g : B \rightarrow A\), definiert durch \(g(b) := b - 3\) für alle \(b \in B\), sodass \((g \circ f)(a) = g(f(a)) = g(a + 3) = a + 3 - 3 = a\) und \((f \circ g)(b) = f(g(b)) = f(b - 3) = b - 3 + 3 = b\) ist.

Satz: Zusammenhang zwischen Bijektivität und Invertierbarkeit von Abbildungen

Sei \(f : A \rightarrow B\) eine Abbildung. \(f\) ist genau dann invertierbar, wenn \(f\) bijektiv ist.

Beweis:

\(\Rightarrow\): Sei \(f\) invertierbar. Dann existiert eine Abbildung \(g : B \rightarrow A\), sodass \((g \circ f)(a) = a\) und \((f \circ g)(b) = b\) für alle \(a \in A\) und \(b \in B\) gilt.

Seien \(a, a' \in A\) mit \(f(a) = f(a')\). Wir wenden auf beiden Seiten der Gleichung die inverse Abbildung \(g\) an und erhalten \(g(f(a)) = g(f(a'))\). Wegen \(g(f(a)) = (g \circ f)(a) = a\) und \(g(f(a')) = (g \circ f)(a') = a'\) folgt \(a = a'\). Somit ist \(f\) injektiv.

Sei \(b \in B\) und \(a := g(b)\). Dann ist \(f(a) = f(g(b)) = (f \circ g)(b) = b\). Somit ist \(f\) surjektiv. Aus der Injektivität und der Surjektivität von \(f\) folgt insgesamt die Bijektivität von \(f\).

\(\Leftarrow\): Sei \(f\) bijektiv. Wir müssen zeigen, dass es dann eine Abbildung \(g : B \rightarrow A\) gibt mit \((g \circ f)(a) = a\) und \((f \circ g)(b) = b\) für alle \(a \in A\) und \(b \in B\).

Sei \(b \in B\). Da \(f\) surjektiv ist, gibt es ein \(a \in A\) mit \(f(a) = b\). Da \(f\) injektiv ist, gibt es genau ein solches \(a\). Wir können somit die Funktion \(g\) definieren durch \(g(b) := a\) für alle \(b \in B\), wobei \(a\) das jeweils eindeutig bestimmte Element aus \(A\) mit \(f(a) = b\) ist.

Für diese Funktion \(g\) gilt dann \((g \circ f)(a) = g(f(a)) = g(b) = a\) für alle \(a \in A\) sowie \((f \circ g)(b) = f(g(b)) = f(a) = b\) für alle \(b \in B\). Somit folgt \(g \circ f = id_A\) und \(f \circ g = id_B\) und damit ist \(f\) invertierbar. \(\square\)

Satz: Eindeutigkeit von invertierbaren Abbildungen

Sei \(f : A \rightarrow B\) eine invertierbare Abbildung. Dann ist die Abbildung \(g : B \rightarrow A\) mit \(g \circ f = id_A\) und \(f \circ g = id_B\) eindeutig bestimmt.

Beweis:

Seien \(g : B \rightarrow A\) und \(g' : B \rightarrow A\) Abbildungen mit \(g \circ f = id_A, f \circ g = id_B, g' \circ f = id_A\) und \(f \circ g' = id_B\). Sei \(b \in B\). \(f\) ist invertierbar, also bijektiv. Aus der Bijektivität von \(f\) folgt, dass es genau ein \(a \in A\) gibt mit \(f(a) = b\). Wegen \(g \circ f = id_A = g' \circ f\) folgt \[g(b) = g(f(a)) = (g \circ f)(a) = a\] und \[g'(b) = g'(f(a)) = (g' \circ f)(a) = a\] Somit gilt \(g(b) = g'(b)\) für alle \(b \in B\) und damit \(g = g'\). \(\square\)

Definition: Inverse Abbildung

Sei \(f : A \rightarrow B\) eine bijektive Abbildung. Die eindeutig bestimmte Abbildung \(g : B \rightarrow A\) mit \(g \circ f = id_A\) und \(f \circ g = id_B\) wird die zu \(f\) inverse Abbildung (oder Umkehrfunktion) genannt und mit \(f^{-1}\) bezeichnet.

Beispiele: Inverse Abbildungen

1. Sei \(f : \mathbb{R} \rightarrow \mathbb{R}_+\) mit \(f(x) := x^2\). Weil \(f\) nicht bijektiv ist, besitzt \(f\) keine Umkehrfunktion. Dies veranschaulicht man sich leicht, indem man sich fragt, welchen Wert eine potenzielle Umkehrfunktion \(g\) z.B. für 1 annehmen würde. Wegen \(f(1) = 1 = f(-1)\) könnte \(g(1) = 1\) sein, es könnte aber auch \(g(1) = -1\) sein. Es ist demnach nicht möglich, eine eindeutige Umkehrfunktion anzugeben.


2. Sei \(f : \mathbb{R}_+ \rightarrow \mathbb{R}_+\) mit \(f(x) := x^2\). In diesem Fall ist \(f\) aufgrund des eingeschränkten Definitionsbereichs bijektiv und besitzt demnach eine Umkehrfunktion. Diese ist gegeben durch \(g : \mathbb{R}_+ \rightarrow \mathbb{R}_+\) mit \(g(x) := \sqrt{x}\). Es ist \((g \circ f)(x) = g(f(x)) = g(x^2) = \sqrt{x^2} = x\) und \((f \circ g)(x) = f(g(x)) = f(\sqrt{x}) = \sqrt{x}^2 = x\) für alle \(x \in \mathbb{R}_+\).

Satz: Bijektivität der Komposition

Seien \(A, B\) und \(C\) nichtleere Mengen und seien \(f : A \rightarrow B\) und \(g : B \rightarrow C\) Abbildungen. Wenn \(f\) und \(g\) bijektiv sind, dann ist auch \(g \circ f\) bijektiv.

Beweis:

Seien \(f\) und \(g\) bijektive Abbildungen. Damit sind \(f\) und \(g\) invertierbar. Sei \(f^{-1}\) die inverse Abbildung zu \(f\) und sei \(g^{-1}\) die inverse Abbildung zu \(g\).

Um zu beweisen, dass \(g \circ f\) bijektiv ist, werden wir zeigen, dass \(g \circ f\) invertierbar ist. Daraus folgt dann mit dem obigen Satz die Bijektivität. Wir zeigen, dass \(f^{-1} \circ g^{-1} : C \rightarrow A\) die inverse Abbildung zu \(g \circ f\) ist:

Wegen der Assoziativität von \(\circ\) ist \((g \circ f) \circ (f^{-1} \circ g^{-1}) = g \circ ((f \circ f^{-1}) \circ g^{-1})\). Wegen \(f \circ f^{-1} = id_B\) und \(id_B \circ g^{-1} = g^{-1}\) folgt daraus weiter \(g \circ ((f \circ f^{-1}) \circ g^{-1}) = g \circ (id_B \circ g^{-1}) = g \circ g^{-1} = id_C\). Insgesamt gilt somit \((g \circ f) \circ (f^{-1} \circ g^{-1}) = id_C\).

Vollkommen analog gilt \((f^{-1} \circ g^{-1}) \circ (g \circ f) = f^{-1} \circ ((g^{-1} \circ g) \circ f) = f^{-1} \circ (id_B \circ f) = f^{-1} \circ f = id_A\).

Folglich ist \(f^{-1} \circ g^{-1}\) die inverse Abbildung zu \(g \circ f\). Die Abbildung \(g \circ f\) ist somit invertierbar und damit bijektiv. \(\square\)

Satz: Bijektivität der inversen Abbildung

Sei \(f : A \rightarrow B\) eine bijektive Abbildung. Dann ist die zu \(f\) inverse Abbildung \(f^{-1}\) ebenfalls bijektiv.

Beweis:

Wir haben oben gezeigt, dass eine Abbildung genau dann bijektiv ist, wenn sie invertierbar ist. Offenbar ist \(f^{-1}\) invertierbar, denn die zu \(f^{-1}\) inverse Abbildung ist \(f\). Folglich ist \(f^{-1}\) auch bijektiv. \(\square\)