

Im ersten Teil des betrieblichen Kernprozesses müssen die Materialien beschafft werden, die für die Erstellung eines Produkts oder einer Dienstleistung im Rahmen der Produktion benötigt werden. Im Zentrum der operativen Beschaffungsaufgaben stehen die Bedarfsermittlung, die Bestellmengenplanung und die Beschaffungsabwicklung. Im Rahmen der strategischen Beschaffungsaufgaben werden die Rahmenbedingungen für die operative Beschaffung gestaltet. So sind Beschaffungsstrategien für einzelne Güter festzulegen, wie z. B. die Auswahl des Beschaffungsmarktes oder die Anzahl der Lieferantenbeziehungen.
Bei der Festlegung der zeitlichen Bereitstellung der Materialien wird zudem eine Verbindung zwischen strategischer und operativer Ebene deutlich, da die Bestellmengenplanung nur im Falle einer Beschaffung auf Lager relevant wird. Da die beschafften und gelieferten Materialien nicht sofort in den Produktionsprozess eingesetzt werden, stellt die Lagerhaltung die Kontinuität des Materialflusses sicher. Dennoch bedarf es einer ständigen Analyse und Planung, bezogen auf Bestellmenge, Verbrauch und Bestellzeitpunkt, um Risiken von materialbedingten Produktionsausfällen zu vermeiden.
Die Beschaffung ist der erste Teil des betrieblichen Kernprozesses. "Als oberstes Ziel der Beschaffung kann die langfristige Sicherstellung der anforderungsgerechten Versorgung zu geringstmöglichen Kosten formuliert werden".
Es muss einerseits sichergestellt werden, dass das richtige Material in der richtigen Menge zum richtigen Zeitpunkt und in der richtigen
Qualität am richtigen Ort zur Verfügung steht. Andererseits müssen die zu beschaffenden Materialien auch möglichst
kostengünstig beschafft werden.
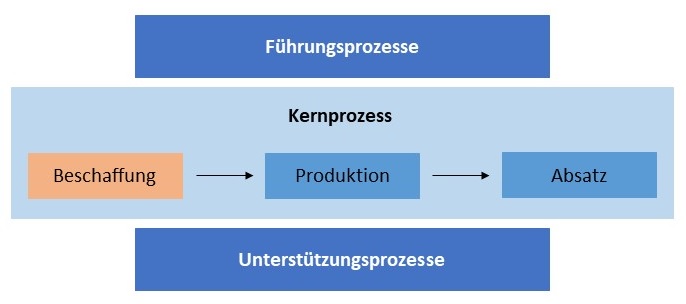
Die Aufgabenfelder der Beschaffung lassen sich in strategische und operative Aufgaben unterteilen.
Zu den operativen Beschaffungsaufgaben im Rahmen der Materialdisposition zählen die Bedarfsermittlung und Bestellmengenplanung sowie die Bestellabwicklung. Bei der Bedarfsermittlung gilt es, die Materialbedarfe der Produktion für einen bestimmten Planungszeitraum unter Berücksichtigung etwaiger Lagerbestände zu bestimmen. Sofern eine Vorratsbeschaffung erfolgt, werden diese Bedarfsmengen auf Bestellmengen und Bestellzeitpunkte im Rahmen der Bestellmengenplanung verteilt. Die Bestellabwicklung umfasst die Bestelldurchführung, die Bestellüberwachung und den Wareneingang.
Materialdisposition:

Die Bedarfsermittlung kann auf zwei Arten erfolgen. Einerseits kann auf Basis von Verbräuchen in der Vergangenheit eine Bedarfsprognose durchgeführt werden (stochastische bzw. auch verbrauchsorientierte Bedarfsermittlung), andererseits können die Bedarfe auf Basis der Planung der herzustellenden Produktmengen über Stücklisten (Produktionsprogrammplanung) errechnet werden (deterministische bzw. auch programmorientierte Bedarfsermittlung). Im Folgenden soll nur ein erster Einblick in die Bedarfsprognose erfolgen.
Ziel der Bedarfsprognose ist es, die Materialmengen möglichst genau vorauszusagen, damit nicht zu große Materialmengen angeschafft werden, die zu hohen Lagerhaltungskosten führen, oder zu wenig Material beschafft wird, sodass der Produktionsplan aufgrund fehlenden Materials nicht eingehalten werden kann.
Prognosemodelle können für einen stationären, einen trendförmigen oder einen saisonalen Verlauf des Materialverbrauchs angewandt und unterschieden werden. Geglättete Prognosen sind für alle (prognostizierbaren) Verlaufsformen einsetzbar, da die Glättung bewirken soll, dass zufällige Ausreißer des Materialverbrauchs nicht zu viel Gewicht bei der Berechnung des Prognosewerts erhalten.
Eine geglättete Prognose ist die exponentielle Glättung. Bei diesem Verfahren verlieren die älteren Vergangenheitswerte über den gewählten Gewichtungsfaktor an Bedeutung. Veränderungen im Bedarfsverlauf werden somit schneller in der Bedarfsprognose berücksichtigt.
Wird von einem konstanten Materialbedarfsverlauf ausgegangen, um den die tatsächlichen Verbräuche zufällig schwanken, so kann die exponentielle Glättung erster Ordnung als Prognoseverfahren eingesetzt werden. Hierbei wird der Prognosewert für die folgende Periode - z. B. Jahr, Quartal, Woche oder auch Tag - als gewichtete Summe aus dem Beobachtungswert der aktuellen Periode (realer Wert) und dem ermittelten Prognosewert für die aktuelle Periode ermittelt (rekursive Form).
Der Prognosewert der betrachteten Zeitperiode ergibt sich aus dem mit \(\alpha\) gewichteten realen, aktuellen Beobachtungswert und dem mit \(1-\alpha\) gewichteten Prognosewert der vorherigen Zeitperiode.
\[\hat{x}_{t, t+1} = \alpha \cdot x_t + (1-\alpha) \cdot \hat{x}_{t-1,t}\]
Je kleiner \(\alpha\) ist, desto weniger werden die aktuellen Beobachtungswerte einen Einfluss auf das Gesamtergebnis haben. Beispielsweise ist bei \(\alpha = 0,1\) die Anpassung an geänderte Daten schwach, bei einem Wert für \(\alpha = 0,7\) ist die Anpassung an geänderte Daten groß. Mit einem hohen Wert von \(\alpha\) geht aber auch einher, dass etwaige größere zufällige Schwankungen entsprechend stärker im Prognosewert berücksichtigt werden.
Beispiel
Verbrauchswerte
| Zeitperiode t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bedarf xt | 22 | 26 | 24 | 29 | 21 | 28 | 31 | 34 | 32 | 30 | 32 | 35 |
In der Tabelle stehen die Bedarfe eines Materials in den vergangenen 12 Monaten des letzten Jahres. Um nun den Prognosewert für den Zeitpunkt 13 (erster Monat des nächsten Jahres) mittels der exponentiellen Glättung erster Ordnung zu ermitteln, muss der Prognosewert für den Zeitpunkt 12 bekannt sein. Aufgrund der rekursiven Form müssen daher zunächst Prognosewerte für alle Vorperioden ermittelt werden, und es bedarf eines Startwerts für den Prognosewert für den Zeitpunkt 1. Für den Anfangswert \(\hat{x}_{0,1}\) zieht man typischerweise den Beobachtungswert im Zeitpunkt 1 heran, dies wäre \(x_1=22\). Der Glättungsparameter soll beispielhaft mit \(\alpha = 0,3\) festgelegt werden.
Die weiteren Werte (gerundet auf eine Dezimalstelle) werden dann berechnet nach der Formel:
\(\hat{x}_{t, t+1} = \alpha \cdot x_t + (1-\alpha) \cdot \hat{x}_{t-1,t}\)
\(\hat{x}_{0,1} = 22\) (als Startwert)
\(\hat{x}_{1,2} = 0,3 \cdot 22 + (1 - 0,3) \cdot 22 = 6,6 + 15,4 = 22\)
\(\hat{x}_{2,3} = 0,3 \cdot 26 + (1 - 0,3) \cdot 22 = 7,8 + 15,4 = 23,2\)
...
\(\hat{x}_{9,10} = 0,3 \cdot 32 + (1 - 0,3) \cdot 29 = 9,6 + 20,3 = 29,9\)
\(\hat{x}_{10,11} = 0,3 \cdot 30 + (1 - 0,3) \cdot 29,9 = 9 + 20,9 = 29,9\)
\(\hat{x}_{11,12} = 0,3 \cdot 32 + (1 - 0,3) \cdot 29,9 = 9,6 + 20,9 = 30,5\)
\(\hat{x}_{12,13} = 0,3 \cdot 35 + (1 - 0,3) \cdot 30,5 = 10,5 + 21,4 = 31,9\)
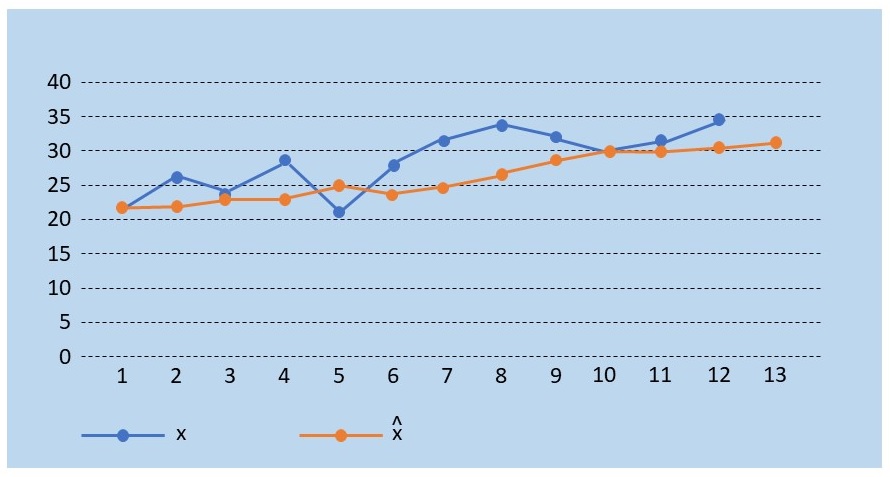
Verbrauchswerte \(x\) und geglättete Prognosewerte \(\hat{x}\):
Soll eine Bedarfsprognose für einen trendförmigen Bedarfsverlauf vorgenommen werden, bieten sich Verfahren der exponentiellen Glättung zweiter Ordnung an.